

This document has a standard, validated CSS2 stylesheet, which your browser does not seem to display properly. In a browser supporting web standards, this table of contents would be fixed at the side of the page for easy reference.
anastigmatix home start FretFocus Java upgrade alertnote: links to other sites from this page are set up to open in a separate window. if nothing seems to happen when you click them, maybe the new window is disabled in your preferences, or it is minimized or behind something else.
FretFocus is a design recovery aid that can be used on-line to reconstruct the design scale length and nut compensation for any fretted, equal-tempered, stringed instrument from a series of simple measurements. At the same time, it gives quantitative feedback on the accuracy of the fretboard and measurement uncertainty. The FretFocus analysis of an instrument can be saved for later use, or printed and sent home with the instrument.
A Java applet, FretFocus doesn't need any special installation: if you can see it in your web browser, you're already running it. (OK, in some cases, you might need a Java plugin first, but FretFocus even tries to help with that part, so just go ahead and try it for starters, and if that doesn't work, then you can read the fine print.)
While several other on-line fret calculators can be found on the Web, most are geared to original construction: given the design scale length for an instrument, they will calculate the appropriate spacing of frets, and some will also suggest the compensation distance at the saddle. The challenge of the reverse direction was pointed out by Sondra Lewis and Frank Ford in a FRETS.COM FAQ entry:
In a nutshell, a builder had a certain scale length in mind, and built an instrument around it, laying out frets and adjusting some dimensions to achieve the right compensation at the saddle and maybe the nut too. By the time you have to work on a finished instrument, you are looking at the combined effect of these design values. How do you tease them apart? You may know the manufacturer's stated scale length, but how accurately does it tell you what really got built? How do you determine, as carefully as possible with available tools and reasonable effort, the true scale length of the instrument sitting on the bench right now?
Techniques that answer that kind of question are sometimes called design recovery. Bringing together principles of equal temperament, compensation and fret layout, measurement and experiment design, FretFocus does that for fretted instruments.
Frank Ford doesn't know it yet, but it's his fault. I happened to be looking for a luthier, and I happened to stumble on his not-to-be-missed FRETS.COM web site, and realized I had found not only a shop I could recommend in a New York minute, but also an answer to a question long at the back of my mind.
I've never been quite sure what to say at all those conversational moments when someone learns I'm a math/CS type, and asks with a wrinkled nose, “why would anyone find that stuff interesting?” I could fumble for an answer, but it's more fun to meet people who already know it, and maybe it's not so surprising, the places you find them. Lutherie is about making beautiful things well, and you can't look around FRETS.COM without seeing the hand of someone to whom nothing is uninteresting if it can help do that better. That is the answer, isn't it? Maybe for luthiers it's an occupational hazard: in this article by Paul Jacobson you see the same curiosity to draw on anything that can contribute to his art, even if it makes him look a tiny bit like a geek. A friend of mine has the word redavinator for such people, as profound a term of respect as any made-up word ever was.
Anyway, I share the love of seeing the right tool for a job—one that I still can't stop grinning over is Frank Ford's spin sander—and it was kind of a treat to see an opening for a tool the luthier community didn't seem to have yet, and realize I had an idea how it could be built, and I was looking for an excuse to learn to write applets anyway. Building tools is the same pleasure whatever the materials you use to do it; those of us who push words and symbols together usually don't have to wear dust masks, but it's the same idea. If FretFocus turns out to be useful, think of it as a tip of the hat from one redavinator to another.
Sondra Lewis already pointed out the problem with this one, in her question. Compensation means the saddle isn't located right at the theoretical end of the scale, and anyway it's slanted, so where do you measure? Throw in that you may also have nut compensation on the other end, and you're nailing Jell-O to a wall. Note to redavinators: if you ever have to do this, here's Clifford Stoll's approach: “First nail the slab of Jell-O to a horizontal board with a grid of ten-penny nails, spaced an inch apart. Then tip the board up and nail it to the wall.”
This seems to be the most common approach in practice. There's a handy tool called the Saddlematic that is based on this approach. What are the shortcomings?
Hmm, now this could be leading somewhere. The reason the nut-to-12th-fret measurement sounds appealing is just that the arithmetic is simple to do in your head. To turn the measurement into the scale length, just multiply by 2.
But really, a measurement between any two frets can give you the scale length. If you have a very precise measurement to the 1st fret, and don't mind ignoring nut compensation, just multiply by 17.817. If your measurement is from the 1st to 2nd fret—and now you can ignore nut compensation—multiply by 18.877. Or measure from the 8th to the 13th fret and multiply by 6.3282. It would be tedious to work out these values by hand, but they all come from the same formula that gave us 2 for the nut to the 12th fret. If you're not anxious to crunch those numbers in your head, why not use a computer, which has no trouble finding the multiplier for any two frets you care to choose, even for non-12-tone experimental instruments, and all more precisely than my rounded examples here?
This way of looking at it lets us pick any two frets on the fretboard and get a measurement that does not involve the nut compensation, and fits the jaws of the best caliper on hand. This will give an answer for the scale length all by itself, apart from compensation, which can now be pinned down separately.
That last idea was definitely getting somewhere. It's almost too much fun. If the computer can solve the scale length given any pair of frets, how about making a bunch of measurements, between different fret pairs, on the same instrument? They should all lead to the same scale length answer, right?
On God's workbench, they would. For the rest of us, they never quite will. For starters, the frets were laid out originally by a mathematical formula, but they were installed with saws and hammers in a hunk of tropical hardwood. Then too, that caliper may be a fine piece of gear, but it has its own limitations. Finally, there are variables in the technique and consistency of the person making and reading the measurements.
All this means is that any measurement of the scale length—any measurement of anything, for that matter—will be slightly uncertain. To make one measurement with an expensive tool, crank through a formula, and stop at one answer can foster a happy illusion of precision. The illusion won't hold up to more data.
On the bright side, the loss of innocence can bring wisdom (at least if you do it right). The coziness of working out one answer, looking no further, and thinking it's the answer, masks a pretty serious problem: you don't get a clear idea how far wrong your answer could be. You could ignore uncertainty and embrace your one answer with stalwart and unjustified confidence. You could wring your hands because you know your measurement was imperfect but not how imperfect or what to do about it. Now, not limited to just one measurement, you have a third option: you can take some more.
The Marines have a saying: Pain is weakness leaving the body.
As you start to take more measurements at different frets on the same
instrument and convert them to scale lengths, the first thing you notice
is how different the answers are. It kind of hurts after that first answer
looked so precise, but that's just the false
confidence leaving your measurement. In its place, after recording
several measurements, FretFocus offers something better:
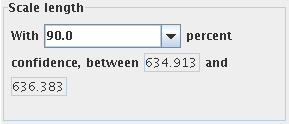
It looks reasonable to say this guitar was meant to have a 635 mm scale, though if I had to locate a saddle or bridge to best match the fretboard as built, I would shoot for about 635.6 from an uncompensated nut. This picture doesn't show the nut compensation figure, but FretFocus gave a range of 0.4–0.9 for that, so it's possible the manufacturer meant 635 exactly to be the scale length measured from the compensated nut. (FretFocus doesn't insist on inches, millimeters, or anything else; if the input measurements are in furlongs, so are the results.)
What happens if I keep the same set of measurements but ask FretFocus for
more than 90 percent confidence?

FretFocus has widened the interval slightly, which makes sense if I've just asked for an answer I can have even more confidence in, and so FretFocus is being slightly more cautious in its commitments. The rule is, for the same set of measurements, I get a wider interval by asking for higher confidence, a narrower interval by asking for less.
Another way to think about these results is to start with the interval width I'm willing to tolerate. Suppose with the materials and construction methods available there'd just be no point in knowing these results to inside a quarter millimeter. So I can see what confidence setting gives me a quarter-millimeter interval on the result. For this guitar and these measurements, that's about 60% confidence on the nut compensation, and 23% on the scale length. If I want to improve that, I need to give FretFocus more or better data. Or, I might just decide that quarter-millimeter precision for the scale length is asking a lot, considering all the flexibility of the neck and top, the fit of saddle in bridge, and so on, and decide I'll tolerate half a millimeter, which gets me to 44% confidence without taking more measurements.
The narrowest interval you can get from FretFocus is the one you get by setting confidence to zero: then FretFocus shows the same number in both boxes. That is the best number to use (according to the measurements you've got) when you feel like saying “just tell me where I should try to put this saddle!”—but this setting hides everything FretFocus knows about how tight that number really is.
There's a way to think about FretFocus's confidence intervals that would not be quite right, and that would be to think that the scale length of the instrument sitting in front of you has a certain chance of being in the interval FretFocus picked, and the confidence setting tells you what that chance is. If that were what the confidence setting meant, then in my half-millimeter tolerance example above, you would look at the 44% confidence and think the scale length was more likely to be outside the result interval than in it! Here's the better way to understand it: the result from FretFocus is always the best fit based on the measurements you've given, but the confidence tells you something about the wisdom of relying only on FretFocus and those measurements as a matter of course.
You can't ask FretFocus for 100% confidence, but you can set 99.999% or even higher, enough to have a long career in lutherie without having to question a FretFocus result. The trouble with that is FretFocus might be giving you intervals half an inch wide—that's why you'd never question one, because you could measure that closely one-handed with a yardstick and plainly see it was right.
To get real value from FretFocus, naturally you'll use it to pin down values more closely than what you can plainly see, and you will soon have a sense of what levels of confidence are realistic for typical jobs, and how much they may vary from one job to another. If you get a result with unusually low confidence, you might budget extra time on that job for final intonation checking, or recognize that you may be looking at a somewhat irregular fretboard and there won't be much you can do about it. You might increase your own confidence by comparing the FretFocus result to the builder's specification, information FretFocus doesn't have. Last but not least, you might increase the confidence from FretFocus by investing a little time in extra measurements.
A natural question for FretFocus is how to get a tighter result, that is, one with a narrower interval at the same confidence setting, or the same interval at a higher setting. Here are some of the factors in play:
To quickly get an idea how all these factors influence the results you can get from FretFocus, before measuring a bunch of real instruments, you can try the FretFocus Simulator. I also recommend reading How Not to Get Tighter Results.
Lots of on-line fret calculators exist on the web. By and large, they tackle a different job: when you know the scale length, they calculate the fret spacing. Here is a (certainly incomplete) sample:
One fret calculator out there deserves special mention, for tackling an especially sophisticated problem and being astoundingly cool: Kenneth Medin's fret calculator is for working with movable-fret instruments and shifting them into different historic (non-equal) temperaments. With a MIDI output it will demonstrate how the adjusted instrument will sound. Written for Atari but can be downloaded and run on Windows or other systems with available Atari emulation software.
Another tool, Aaron Spike's FretFind, seems to be similarly ambitious: the 2-D version models the frets and strings as line segments in 2-D that do not have to be parallel or equal in length. It can do fan-fretted and other experimental instruments, and also seems to have MIDI auditions in the works.
FretFocus uses your measurements, entered as shown here
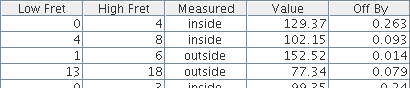 with the nut considered fret zero, to
compute best-fit values for the scale length, nut compensation, and (as
you will see) fret width. The Off By column deserves
special mention: you don't enter these numbers, FretFocus
displays them as the difference between each of your measurements and what
that measurement ideally would be according to the best-fit solution.
These differences are also called residuals, and if you square them
all (which makes them positive) and add them up,
you get a measure of how far from perfect the fit
is. FretFocus does that for you, and chooses a result so the
sum of squares is smallest; thanks to
Carl Gauss for the idea.
with the nut considered fret zero, to
compute best-fit values for the scale length, nut compensation, and (as
you will see) fret width. The Off By column deserves
special mention: you don't enter these numbers, FretFocus
displays them as the difference between each of your measurements and what
that measurement ideally would be according to the best-fit solution.
These differences are also called residuals, and if you square them
all (which makes them positive) and add them up,
you get a measure of how far from perfect the fit
is. FretFocus does that for you, and chooses a result so the
sum of squares is smallest; thanks to
Carl Gauss for the idea.
Suppose you measure between fret f1 and fret f2, and you get measurement m. Your measurement is related to the scale length s this way:
m = t(f1,f2) s
where t(f1,f2) is a number FretFocus can calculate knowing only f1 and f2 and your number of equal-tempered frets per octave (twelve, unless you have some wild experimental instrument). Just how to compute t(f1,f2) I'll save for an appendix, but one point is important here: f1 and f2 are known, so t(f1,f2) is a simple constant once FretFocus computes it. That means the equation above is just a simple linear equation like m = k s, though t itself is nonlinear. As a familiar example, t(0,12) for a standard instrument is exactly one half.
The way you hear people use linear and nonlinear these days, you're probably expecting me to say something like new paradigm or out of the box next! Fear not; I still just use them to mean whether something makes a straight line when you graph it. The equation above does, when f1 and f2 are known, even though t(f1,f2) itself makes a curvy surface. It makes a difference in which solution techniques work best, so it's useful to know, but to really enthrall a cocktail party you've got to throw in some overcomplicated hand-waving and mixed-up metaphors, which you can easily find elsewhere.
There is only one unknown, so one measurement would be enough to solve that equation for s and get a single answer. With more than one measurement, FretFocus has a system of linear equations. A system with more equations than unknowns is overdetermined—there's no guarantee of an exact solution to perfectly satisfy all the equations at once, but there will be a solution that fits best by least squares.
The slight offset of the nut toward the first fret—the nut compensation c—only affects measurements made from the nut ("fret zero"). Those measurements will be shorter by c:
m = t(f1,f2) s + (-1)c when f1 is 0 m = t(f1,f2) s + (0)c in any other case
The new equations have two unknowns, s and c, but are still linear, and FretFocus can solve them with the same technique, though it now needs at least two measurements to get started.
All the equations so far have assumed exact measurements from the midline of one fret to the midline of another. That would work, but those measurements may be hard to make. It's easy to snug a caliper across the outsides of two frets, or against the insides, but center measurements would mean trying to set the points right on the centers of nice rounded frets, which would not make the best use of a precision instrument. Maybe a specialized mechanical tool could be built for measuring at the exact centers of frets, but it would probably be expensive and delicate to use. FretFocus takes a lazier approach: just use the commonly-available measuring tool in the easiest way, and let the computer make the needed corrections.
A measurement inside two frets is shorter than the exact midline measurement by one fret width w (half at each fret). A measurement outside two frets is longer than the midline measurement, again by exactly w. As a special case, an inside measurement from the nut to a fret is shorter by just half w, at the real fret, as long as the nut side of the measurement is right where the string breaks over.
m = t(f1,f2) s + (-1)c + (-1/2)w when f1 is 0 m = t(f1,f2) s + (0)c + (-1)w for any other inside measurement m = t(f1,f2) s + (0)c + (1)w for any outside measurement
Because this is still nothing but a system of linear equations, now with three unknowns, FretFocus doesn't need to be told the fret width before it can find the scale length and compensation: it just finds the best-fit solution for all three at once, as long as you provide enough simple measurements inside and outside different frets and the nut. However, unless the fretboard is made to very tight tolerances, you can often get tighter results in fewer measurements if you do supply your own careful fret width measurement.
With a little thought to making measurements as consistently as you can, you
will help FretFocus produce tight results. For a good indication of how you
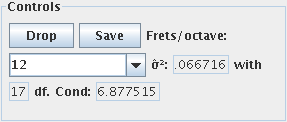
are doing, you can look at this number from the Controls pane:
 A lower number is
tighter. This estimate of variance is directly related to the confidence
intervals around your results: if you can cut this number in half, those
intervals get half as wide, other things being equal. Part of what this
number measures is variation in the placement of frets themselves, which it's
too late to change, but part of it is variation in your measurement
technique, and you can try to hold that down so at least you get the tightest
results you can for a given fretboard.
A lower number is
tighter. This estimate of variance is directly related to the confidence
intervals around your results: if you can cut this number in half, those
intervals get half as wide, other things being equal. Part of what this
number measures is variation in the placement of frets themselves, which it's
too late to change, but part of it is variation in your measurement
technique, and you can try to hold that down so at least you get the tightest
results you can for a given fretboard.
You might want to make sure that all of the measurements entered into FretFocus for a particular instrument were taken by one person, using one measurement tool. That will keep at bay personal differences of measurement technique and slight differences between tools. It's also helpful to cultivate one consistent technique for setting and reading the caliper and getting a reading perpendicular to the frets (I like to rest the caliper points lightly against the D or G string). By taking the measurements close together in time, you can minimize any changes of temperature or humidity between them.
One tip for taking tight measurements might be: take more large ones than small ones. For example, if a caliper has 150 mm jaws, you might consider taking more measurements across several frets than across one or two. Here's the idea: your uncertainty in reading the caliper might be around a hundredth of a millimeter or so, and it doesn't depend on whether you're reading a large distance or a small one—but it makes up a smaller proportion of the longer reading than of the shorter one.
That tip can be taken overboard, though. If you make only measurements out near the maximum reach of your caliper, you can wind up giving FretFocus a series of measurements that are all very similar and, as the next section explains, that isn't ideal.
Suppose you give FretFocus a list of measurements without any including the nut. In this case FretFocus has no information at all to find one of its three unknowns, the nut compensation. FretFocus can tell it simply hasn't got enough information to work from, and the results will stay grayed out until you have added at least one measurement from the nut. Then it will show a result, but you can surely tighten it by adding a few more measurements from the nut to different frets.
Now suppose you have a bunch of measurements, but they are all inside measurements, made with the caliper jaws against the facing sides of two frets. Here FretFocus has a tough job finding the fret width. The results are not grayed out, because FretFocus does have something to go on: the inside measurements will all be slightly different from what perfect midline measurements would be, and that is enough to take a stab at the fret width. The trouble is, the measurements also vary because of fretboard imperfections and your measurement technique, and with FretFocus trying to infer fret width from fairly tiny differences to begin with, it may be thrown quite off by these other variations. With a mix of some inside and some outside measurements, FretFocus could do a much better job.
The same kind of issue comes up if you have many measurements that are not much different. For example, a measurement from frets one to six and one from frets six to thirteen will be very close, even though one spans only five frets and one spans seven. If FretFocus has only a bunch of very similar measurements to work from, it will depend on very small differences between them to sort out the effects of scale length and fret width. In the last section, I suggested that longer measurements are preferable to shorter ones because the uncertainty in reading the caliper is a smaller part of the total measurement, but that has to be balanced with giving FretFocus a healthy mix of some shorter and some longer measurements.
To see how you are doing in this area, take a look at this number in the
Controls pane:  The condition number is an estimate
of how sensitively FretFocus's results depend on tiny changes in the
measurements, so you would like this number to be low. The number can get
rather high if you have given FretFocus a poor variety of measurements to
work from, and you can see it come down dramatically by throwing in a few new
measurements that give a better mix: inside measurements if you have mostly
outside ones, short ones if you have mostly long ones, and so on.
The condition number is an estimate
of how sensitively FretFocus's results depend on tiny changes in the
measurements, so you would like this number to be low. The number can get
rather high if you have given FretFocus a poor variety of measurements to
work from, and you can see it come down dramatically by throwing in a few new
measurements that give a better mix: inside measurements if you have mostly
outside ones, short ones if you have mostly long ones, and so on.
Here's an idea that has worked pretty well for me, in the sense of getting a nice low condition number and decent results. I make several inside measurements from the nut: nut to fret one, on up to the farthest fret my caliper can reach. Then I take a few more measurements up the neck spanning that same number of frets, which assures me some progressively smaller measurements as I go. Then I get a few outside measurements the same way, starting with fret one to the farthest I can reach, then measuring a few spans of the same number of frets up the neck. Feel free to experiment to find a procedure that gives you acceptable results and a low condition number without requiring too many measurements.
It can be handy to work out a consistent routine for which measurements to take at which frets, fill in a FretFocus session with those measurements, and save it to use as a template for measuring other instruments later. That way, data entry boils down to changing the numbers in only one column. To avoid losing your place in the column, it may help to save your template session with obviously bogus numbers, like zero, in that column. That will cause FretFocus to give very bizarre results during your later entry, while you have a mix of real and bogus numbers in the column, but only until you plug in the last real one.
Two of the unknowns FretFocus finds, the scale length and the nut compensation, are things you can't directly measure; after all, that's what it's for. But it also solves for fret width, which you can measure yourself, and you may find that FretFocus has not come as close as you did. That's because FretFocus minimizes the sum of squared residuals of total measurements, where scale length plays a much bigger part than fret width. You may find it easier to get tight results if you use an experimental FretFocus feature that lets you supply the fret width you have measured yourself.
To use the feature, just measure the fret width and enter it in the natural way: as an outside measurement where Low Fret and High Fret are the same—the fret whose width you measured. FretFocus treats such an entry specially: instead of thinking (fret width) = (measurement), it thinks 100(fret width) = 100(measurement). That will very strongly encourage FretFocus to find a solution whose fret width matches your measurement, and this may slightly improve the solutions for the other two unknowns. You can get an idea of what difference this feature can make by trying the FretFocus Simulator.
The feature is experimental because I would need to find a real statistician to figure out how meaningful the statistical results—variance and confidence intervals—are when the feature is used. You would certainly disregard FretFocus's confidence interval for the fret width itself, because you came up with the number, not FretFocus. My educated guess is the intervals for scale and compensation are still about right. I don't yet know enough to guarantee it, but then FretFocus is free and I don't guarantee anything else about it either, so maybe that's ok. You will notice the condition number increase when you use this feature, maybe into the low hundreds, but that is nothing FretFocus can't handle.
I think there's some literature on better ways to solve least squares problems where you already know something about the solution, and when I learn more about those, this feature will probably be replaced with something better. I think it was even covered in the Lawson and Hanson book, but it's nearly always checked out at the library and I haven't had my hands on it since the first time.
The variance that FretFocus estimates
( ) can be brought only
so low by perfecting your measurement technique. What's left reflects the
imprecision in the layout of the fretboard itself, with a lower variance
reflecting tighter tolerances.
That suggests it might be interesting to see just how much the variance
really differs between instruments of various categories: factory-built
versus hand-built, inexpensive versus premium, even between different
instruments of the same model.
I don't have access to a wide selection of guitars of different makes and
prices, but a luthiery might accumulate some interesting results over time.
) can be brought only
so low by perfecting your measurement technique. What's left reflects the
imprecision in the layout of the fretboard itself, with a lower variance
reflecting tighter tolerances.
That suggests it might be interesting to see just how much the variance
really differs between instruments of various categories: factory-built
versus hand-built, inexpensive versus premium, even between different
instruments of the same model.
I don't have access to a wide selection of guitars of different makes and
prices, but a luthiery might accumulate some interesting results over time.
Because FretFocus does not separate the variance due to instrument construction from that due to measurement technique and other variables, the only way FretFocus variances can be sensibly compared is between instruments measured in the same luthiery by the same person, in a stable environment, at the same frets, with the same technique. A saved template specifying exactly the measurements and frets to be used for all instruments would definitely be the way to go. Even then, it would be reckless to use comparative FretFocus results for any kind of marketing or promotional purpose. Without much more experience with the range of values that really crop up in lots of real instruments, it's not even possible to say what would or wouldn't be a significant difference, or how it should be interpreted. Moreover, there is a real possibility that FretFocus results could be ‘cooked’ as described in the next section. I don't want to discourage responsibly collecting and even sharing that information, because that's the only way to get the missing experience, but I don't want any guitar makers teed off because somebody reported a 0.08 variance for them and 0.04 for a competitor. As a compromise, I suggest that any comparative variance results be aggregated in terms of generic categories (handbuilt/factory, fretboard material, instrument type/style, era, price range) and not identify makes and models.
After making a number of measurements on an instrument and entering them into FretFocus, you may find that you can get even tighter results by dropping some of the measurements you have made. You will find it works especially well if you drop a few of the measurements with the largest (positive or negative) Off By residuals—that is, the ones that fit least well—and that just a few rounds of strategically discarding data can make your results look tremendously tighter. I hope everyone who tries out FretFocus will try this at least once, to see just how tempting it is, and to understand exactly why it's bogus and, if the results are used for anything, unethical too.
“But wait,” you may protest, “I had complete freedom to choose what measurements I took, and these results are exactly what I would have if I had happened to choose just these measurements to take at the start,” and you would be right. That's the luck of the draw, it's presumed random and unbiased, and it's the reason that equally legitimate studies can report different results. Some may be low, some may be high, but they all had a fair chance to be about right. But once you begin dropping measurements you already have when you don't like what they tell you, bias has found its way in: you have strayed into cooking the data. You have lowered your chances of seeing what's really there, to improve the chances of seeing what you want. This may seem like hairsplitting, but it isn't: yes, the result is the same as one you could have obtained by honest chance, and the fact that you didn't is what makes all the difference.
There are perfectly good reasons for looking at the residuals. If you see one wildly high, by all means recheck to make sure you didn't measure at the wrong frets, or swap two digits reading the caliper, or something like that. If you did, get the right physical measurement, and correct that entry. You might see a pattern where all the measurements with big residuals involve the same fret, and check if that fret was sloppily placed on an otherwise tight board, and choose to leave that one out so you get a better result for the rest of the board—of course you would never do that to get results for comparing to another instrument. Unless a high residual leads you to an obvious mistake or problem, though, a measurement made is a measurement played. It's always ok to make more and see if that tightens the result, but you won't get a better fretboard by discarding measurements that show where it's off.
FretFocus is copyright © 2005 by Chapman Flack and has a home at http://fretfocus.anastigmatix.net/. Permission is hereby granted without fee to use FretFocus for any purpose, and to cache and/or mirror FretFocus and its supporting files to conserve network bandwidth and availability, provided this copyright and permission notice is preserved unaltered, including the link to its original home. The HTML code to embed FretFocus, loading it from its original home or any mirror, may be incorporated in any web page, provided such page clearly identifies the applet as “fretfocus.anastigmatix.net”, provides a usable link thereto, and does not present FretFocus as the work of any other person than its author. FRETFOCUS IS PROVIDED AS-IS WITHOUT EXPRESS OR IMPLIED WARRANTY, AND WITHOUT REPRESENTATION AS TO ITS SUITABILITY FOR ANY PURPOSE.
The following terms apply only to the packages named, which are used by FretFocus and can also be obtained directly from http://dsd.lbl.gov/~hoschek/colt/:
Packages cern.colt* , cern.jet*, cern.clhep
Copyright (c) 1999 CERN - European Organization for Nuclear Research.
Permission to use, copy, modify, distribute and sell this software and its documentation for any purpose is hereby granted without fee, provided that the above copyright notice appear in all copies and that both that copyright notice and this permission notice appear in supporting documentation. CERN makes no representations about the suitability of this software for any purpose. It is provided "as is" without expressed or implied warranty.


When you click  , you get a dialog that lets you enter
information about the instrument, the customer, and the artisan doing
the measurement; all of this is optional, and FretFocus does nothing with
it except include it in the page you can save. You then have two options:
, you get a dialog that lets you enter
information about the instrument, the customer, and the artisan doing
the measurement; all of this is optional, and FretFocus does nothing with
it except include it in the page you can save. You then have two options:


Here are some results from browsers where I've tested the more convenient, cloned-page method:





Each of the three results found by FretFocus—scale length, nut compensation, and fret width—will be displayed in a pane like the one shown. You may choose any confidence level, or select one of the presets (90, 95, or 99 percent). If you enter zero, then both result boxes will display the same number; this is FretFocus's best estimate given the measurements you have supplied, but by doing this you learn nothing about how tight the result really is.
The number of measurements will make a bigger difference at higher confidence levels—or, to say the same thing, changing the confidence setting will have a smaller effect on the results when you have more measurements.
If you have exactly three measurements and FretFocus is able to find a result from them, it has no degrees of freedom to make a confidence estimate. In this case, it will not show a result unless you set confidence to zero (or enter more measurements).

This is where your measurements go. To add another entry, just enter it in the empty last row. A Low Fret of 0 is the nut. To enter inside/outside, you can click in the cell, or tab to it, type a key to get its attention and then type i or o (just typing ii or oo works well). Numbers in the Off By column are reported by FretFocus, not entered. If you are a measuring fiend and take more measurements than there are visible rows, a scrollbar will appear.
There is always an empty last row to allow making a new entry (except while you are making the entry, when the row is only partly empty). The Safari browser gives all of FretFocus a Mac OS makeover, which is beautiful except for one thing: it makes the empty last row completely invisible! You just have to know it's there. Click just beneath the last full row, or beneath the column headings in an empty session, and you can enter data.
If you make an entry FretFocus can't use, the box outline turns red and a reason is shown in your browser's status bar. If you don't see the reason there, just try the same entry again and FretFocus will put the explanation in a pop-up dialog. To me that's kind of distracting, so FretFocus tries the quiet red outline and status message first.
Sometimes FretFocus rejects one entry because it conflicts with an earlier one, and the earlier one is what you need to fix. You can use the escape key to revert the entry FretFocus is rejecting, so that you can go back and fix the other one.
To help you quickly get a sense how different techniques and instrument tolerances affect the results you can expect, FretFocus has a simulator mode that doesn't require real instruments to measure. The FretFocus Simulator has its own page for details and examples.
FretFocus is a Java applet that should, in the best case, just be happily running in your web browser as soon as you look at it. If that doesn't happen, here are some things to look at:
FretFocus should Just Work if your web browser has Java 1.4 or later support built in, or if you have the Java Plugin, 1.4 or later, already installed. Otherwise, FretFocus will try to help you get and download the plugin: if your browser is Internet Explorer, it may offer to download the plugin for you from Sun Microsystems automatically; if you are using Netscape/Mozilla/Firefox, you will probably be taken directly to a plugin download page that will help step you through the process. So, my first suggestion is to just try running FretFocus and wait for one of those helpful things to happen. If you wait and it just doesn't happen, you may need to find the Java plugin yourself. On the bright side, you just do this once, and after that you're all set to run FretFocus or any other web application that uses Java.
Even if you already have a working Java plugin, and FretFocus works fine, please check your plugin version using About Plugins in your browser. If the version is 1.4.2_05 or earlier, you should upgrade it to fix a security issue. FretFocus will work fine whether you upgrade or not, but please make sure you have at least 1.4.2_06 or any 1.5 version just to be safe. If you are downloading the plugin for the first time, you should be fine. Here is Sun's announcement of the issue.
Your browser probably offers a Help: About Plug-Ins menu choice that you can use to check whether you have a Java Plugin already. If you don't, the next section is for you. If you do but it's too old (the display doesn't show version 1.4 support), you still need to get a newer plugin, so read on. If you have a Java plugin that's version 1.4 or later, but FretFocus won't start up anyway, take a look at Have Plugin, Can't Start FretFocus below.
If you already have a JRE 1.4 or later version installed on your computer for any reason, then you don't need to download anything, the plugin files are already on your computer somewhere, and you just need to make sure your browser can find them. As an example, when I installed the JRE on my computer, I was asked to pick a directory/folder name where the software should be installed. After installation, by searching below ‘lib’ and ‘plugin’ in that directory, I found several files with names like ‘libjavaplugin_nscp’ and ‘libjavaplugin_oji’. I looked in my browser's documentation to learn which of those plugin files was the right one for my browser, and then I linked that file into my browser's ‘plugins’ directory. Once I exited and restarted my browser, it found the plugin and I was done. The easiest way to find the browser documentation I needed was just to do a Google search on “java plugin” plus the name of my browser.
If you are sure there is no Java Runtime Environment on your computer already, you can download it from Sun Microsystems. You can click the “Free Download” tab at the top of that page, which will try to determine what kind of computer you have and do all the right things automagically, or choose the right download yourself from the options you see on the page. Once your JRE is installed, you can back up two sections, check if your web browser has found the plugin, and find the right file if it hasn't.
So you tried to start FretFocus, and maybe you saw some promising applet-starting action, but then it just conked out and left you something like a blank rectangle or a broken coffee cup icon. Maybe there is a message on your browser's bottom status line that says “applet failed to start” or the like.
The most important step is to find out what happened. There is probably a way in your browser to open the Java console window (for Mozilla, it's Tools -> Web Development -> Java Console). There are probably messages in that window describing what went wrong. Then it might be easy to see what needs to be done or, if you need to ask for help, the information you saw in the console will be helpful to know.
Obviously, your browser preferences have to allow Java before FretFocus
will work.
A little less obviously (so that's why I'm mentioning it), your preferences
have to allow Javascript for the
 button to work. Check that
preference if everything about FretFocus works except saving.
button to work. Check that
preference if everything about FretFocus works except saving.
Saving still might not work right if you're unlucky in the browser you're using. I used Javascript features that are supposed to be standard, dang it, but apparently they're not widely used and some browser vendors don't get many bug reports about them except from people like me. Mozilla's one browser where it definitely works, but may need the View Source workaround I mentioned in the Reference.
...quite a lot of people who very cleverly worked out tools and techniques for doing things that came up in their own work, and then shared them. In part, there would be no FretFocus without:
Carl Gauss had a day job as an observatory director, and was also involved in surveying Hanover. Both kinds of work involved heaps of uncertain measurements he needed to combine into usable ones, while somehow accounting for the uncertainty of the result. He didn't have the tools to do that, so he built them, and published Theory of the Combination of Observations Least Subject to Errors in 1823, with a supplement in 1828. The least-squares method that he'd been polishing since the turn of the century was a hit with just about everybody who needed to get sound results from uncertain measurements, which was—and still is—pretty much everybody who takes measuring seriously.
Gauss worked out a way to take the overdetermined system of equations—the one that can't be solved exactly because it has too many equations to satisfy—and turn it into a different system with just the right number of equations to have an exact solution. The exact solution of that one is the best least-squares fit of the original.
You might remember how to solve the exact system from high school or college, and if you do, the first method you saw was probably Gaussian elimination. Yes, that was his too. It's not known for certain if the guy ever slept.
To estimate the confidence intervals around the results, there has to be some notion of how the random noise in the original measurements will affect the calculations. The usual assumption is that the measurement errors will follow a normal distribution with lots of small discrepancies and rare larger ones, making that familiar bell-shaped curve. Giving credit where it's due (again!) the normal distribution is also called the Gaussian distribution.
The trouble is, the normal distribution isn't quite right for the confidence intervals on the results, because you only have a small sample of measurements. The right distribution is also bell-shaped, and it gets closer to normal the more measurements you have, but for small samples it's a shorter, wider bell, to allow for variation between different small samples.
The problem was solved by William Gosset in his employment with Guinness, where he had to do quality control and process improvement without being able to sample as much product as he might have liked. Guinness wouldn't let him publish in his own name (maybe so the competition wouldn't catch on that a good statistician was a smart hire for a beer outfit?), so he used the name ‘Student’ on his 1908 papers, and the distribution is called Student's t.
Ronald Fisher's work in genetics led to his interest in statistics. He recognized the importance of Gosset's ideas, and incorporated them with his own work on other distributions, and the notion of degrees of freedom, into the serious study of how to design experiments to get tight results with a reasonable amount of effort.
The programming language I chose for FretFocus developed out of a Sun Microsystems project in 1991 to allow all kinds of odd home devices like cable TV set-top boxes to be programmed in a consistent way. The cable companies weren't interested—not then, anyway—but the Java language took off anyway, and because it did, I can develop FretFocus on my computer and be pretty sure it will run on yours, without having to know much about what kind of computer you've got. One of the important decisions Sun made for Java was to pin down exactly how it would do floating-point arithmetic, no matter what kind of computer it's running on, which helps me be sure FretFocus will give you just the same results it gives me, for the same measurements.
That floating-point arithmetic I just mentioned can be tricky, because it isn't infinitely precise: all the arithmetic in FretFocus gets rounded after about the 14th significant digit. That's plenty and to spare for most reasonable purposes—you're never going to measure a fretboard or locate a saddle with that kind of precision—but the tricky part is that small roundoff effects can snowball through later calculations until the final result is seriously off. The 17.817–17.835 discrepancy is a simple example of that, after just a few steps of arithmetic. FretFocus, under the hood where you don't see it, does a lot more arithmetic than that.
That's a headache, because it means two different formulas to get the same result can be mathematically equivalent, proven, and one of them would work just fine on a computer and the other give a badly wrong answer, just because it does the work in a different order that lets the roundoff error blow up. The tiniest details matter. The simplest approach to solving least squares given by Gauss has exactly that problem (which he could hardly be blamed for, in 1823): nothing wrong with it as pure math, but on a computer it's awful.
The trick is to find other ways to get the wanted result, mathematically equivalent to the simple approach, but practical on a computer because they keep the roundoff error under control. Jim Wilkinson and Alston Householder made huge contributions of that sort during the war effort for the kinds of computation FretFocus needs to do, Wilkinson at the National Physics Laboratory in London, Householder at Oak Ridge National Lab in Tennessee. The Householder reflection technique FretFocus uses neatly avoids magnifying any errors; they're expected to be no bigger in the result than they were in the input.
At last all the methods FretFocus needs are in place, and now the only trouble is they started to get complicated, especially in that last step where the nice straightforward approaches had to be checked for working reliably in computer arithmetic, or replaced with harder ones that do. That kind of programming is very demanding! Even a minor difference between two ‘equivalent’ approaches can spell trouble, and if I had to program Householder reflections, Student's t-distribution, and the rest all from scratch to get FretFocus working, and then test for accuracy and chase down all my mistakes, there's no way I would ever have started.
Thank goodness I never had to do that. The gang at CERN, the European Organization for Nuclear Research, has to do the same kinds of things all the time. Most of what they want to find out can't be directly observed, but has to be worked out from what they can observe, making the best use of tools, experiment time, and budget. FretFocus accounts for fret width so you can make the best use of an available tool instead of having to build some special jig for centerline fret measurements, and ideas like that are even more in demand when the special tool might need a Parliamentary appropriation and take 15 years to build. Needless to say, they have computer scientists working very hard to program all the techniques just described, and many more, at the state of the art in speed and reliability. Even better, they have done some of this in Java, a language they like for the same reasons I do.
Here's the best part: they made an open-source release, so any Java programmer can get the Colt project and start writing programs to solve all sorts of problems, even obscure lutherie ones, using the same techniques and the same software that works at CERN. Because FretFocus uses Colt, the part of FretFocus that really computes the results—the part I had to write—is all of 100 lines long. Most of that just sets things up, and the key line looks like this:
x = QR.solve(b);
Colt does the rest. And all CERN asked of me in return was that I remember to credit them in the terms of use.
CERN sets a great example of a publicly-funded institute giving back to the public that funds it. A dozen years ago, they were giving away software for building what became the World-Wide Web, too.
Purdue made me blunder through courses in numerical analysis even though everybody in my area, systems and programming languages, grumbled about it and wanted it optional and thought it was only useful to other people. Surprise!
Hideo Kamimoto, Complete Guitar Repair, Oak Publications, 1978.
Walter Piston, Harmony, fifth edition, W. W. Norton & Company, 1987.
Douglas C. Montgomery, Design and Analysis of Experiments, fourth edition, John Wiley & Sons, 1997.
John R. Rice, Matrix Computations and Mathematical Software, McGraw-Hill, 1981.
Charles L. Lawson, Richard J. Hanson, Solving Least-Squares Problems, SIAM, 1995.
David Goldberg, What every computer scientist should know about floating-point arithmetic, ACM Computing Surveys 23:1, March 1991, pp. 5–48.
Walter Gautschi, Numerical Analysis: an introduction, Birkhäuser, 1997.
And the many handy links that are sprinkled through this page.
This appendix describes what's behind t(f1,f2), the number FretFocus computes to relate the scale length to the distance between any two frets f1 and f2. It's a long section, for what's really a very small part of FretFocus, and it's divided in two parts. The first part is the more interesting one—unless it's all review—and that's the background idea of equal temperament itself. From that, the needed formula falls out with very little trouble.
The equal-tempered scale is a neat combination of discovery and invention. It starts with a few things we didn't invent, but only learned about our own hearing and the physical world:
In that last point, you might have been wondering how names like octave, fifth, and fourth ever came from the ratios 1/2, 2/3, and 3/4. They didn't. They come from the idea of a musical scale, and that's the invented part. The whole idea of a scale—a sequence of intervals that fit neatly in an octave and then repeat in the next—is exactly what nature didn't provide. Here's an example:
On a 61-note keyboard, you can just manage to start at the lowest note and reach the same note at the high end by playing 12 perfect fourths—C–F, F–Bb, Bb–Eb, Eb–Ab, Ab–Db, Db–Gb, Gb–Cb(B), B–E, E–A, A–D, D–G, G–C—just as if you had played five perfect octaves. But five perfect octaves should be the interval you get if you divide a string's sounding length in half five times, so the final length is ½5 or 1/32 the original length. Twelve perfect fourths would be ¾12 or 531441/16777216, and that is very close to 1/32 but different enough that if you heard both pitches together you would wince. The same thing happens with fifths, thirds, or any of the other non-octave intervals: you never come around to quite match with perfect octaves.
It turns out that musicians like the idea of a scale too much to give it up just because it isn't possible. Better to invent something that works like a scale and still sounds almost right, and out of various approaches the one most widely used today is equal temperament. The idea is simple: invent an interval that, repeated the right number of times, really does come to a perfect octave and, on the way, does not miss by too far the other important intervals like fourths and fifths. Western music settled on an interval that fits twelve times in a perfect octave; seven of that interval will make a decent semblance of a fifth, and five of them are not far from a perfect fourth. The price for twelve-tone equal temperament is to agree to give up the original ratios and just give the names fourth and fifth to what you get by stacking five or seven of this invented pitch interval. The payoff is that any twelve of these 'fourths' really make five octaves, any twelve 'fifths' really make seven octaves, and keyboards and fretted instruments sound just as good (or just as off) in any key.
To invent an interval really means to figure out how to produce it: if you had a stringed instrument, where would you stop the string to make an interval that, repeated twelve times, would raise the pitch an exact octave? You know you'll divide the sounding length of the string by the same number each time, so to divide by this number twelve times has to be the same as to divide by two. That leaves no choice about the number: it's the twelfth root of two, nothing else.
With that out of the way, it's easy to invent a temperament that divides an octave into any number of equal intervals n: the interval is what you'll get as you divide the sounding length of a string by the nth root of two. Not all such temperaments will sound good, but some reportedly do. The difference probably involves how close you can get to the other intervals humans easily recognize.
The natural intervals are defined by convenient ratios like 1/2, 2/3, and 3/4. Not so for the twelfth root of two: not only isn't it a convenient ratio, it isn't any ratio at all (which is all I would mean if I let slip that it's irrational). It's somewhere between 196/185 and 197/185. Even closer, it's somewhere between 2739815/2586041 and 2739816/2586041, but another ratio will always be closer still and yet never quite right. As a decimal, it never ends, but in the first several places it's 1.059463094.... There's just no easy way to write it down, so for short I'll call it r.
The place to put the first fret is right where it would make the sounding length of the string 1/r of its original length. In building a fretboard, it may be easier to measure from the nut end, and think about the silent length of string above the fret instead of the sounding length below. For the silent length, just multiply the original length by (1−1/r), or divide by 1/(1−1/r), which is a number that will look familiar to luthiers. It's another irrational, but to the first several places it's 17.8171537... more familiarly rounded off to 17.817.
Among other on-line fret calculators, there are some that claim a different calculation method. At least one even offers a choice of the "twelfth root of two", "17.817", or "17.835" method. It should be easy to see now that the "twelfth root of two" is exactly what equal temperament is based on, and 17.817 comes directly from it, just by carefully computing 1/(1−1/r) and then rounding the end result to 17.817 for convenience. It should be close enough for instrument building.
What, then, of a "17.835 method"? It's about a tenth of a percent different from 17.817, which might not be audible in how an instrument plays, but where could the number have come from?
The number 17.817 came from 1/(1−1/r) by rounding at the end of the calculation. Now see what happens if instead we start with a rounded value of r: if we throw away all of r after the 1.0594 and then do the same calculation, we get 1/(1−1/1.0594) = 17.8350.... The difference between 17.817 and 17.835 came from rounding r early and carrying the roundoff error through the rest of the work.
This is where Mrs. Silver, my sixth-grade teacher, would surely point out that the right way to round 1.05946... would have been 1.0595, not 1.0594. If she'd had her way, we would also have a "17.807 method" for laying out frets (and yes, Mrs. Silver, that would be closer than 17.835).
When a computer and not a human is doing the work, there's no need to round anything down to a few digits for convenience. FretFocus is written in the Java language, which provides floating-point operations with about 14 decimal digits and accurate functions to find the twelfth (or any) root of two. FretFocus rounds nothing to fewer digits until the end of calculations, for display.
When FretFocus sees measurements from an instrument that was built using rough calculations like 17.835, two things will happen. FretFocus can't tell the difference between a fretboard built with rough calculations and one built with precise calculations and rough workmanship, so in either case the results will be a little less tight than they could be. The scale length will not exactly match the number from the builder, but will be the scale length that best matches the as-built fretboard. For an idea how much difference the approximations make (very little for 17.817, a bit more for 17.835), you can try the FretFocus Simulator.
By this point, the relation between the nut-to-first-fret measurement and the overall scale length has been pretty well beaten into the ground. The first fret should leave a sounding part below it that is the original scale length times 1/r, and a silent part above it that is the scale length times (1−1/r), and either figure is enough to place the fret, though the silent length would be easier to measure. Now what FretFocus needs is a formula for what I earlier called t(f1,f2): the distance from any fret f1 to any fret f2, scale length factored out. (Think of t(f1,f2) either as something to multiply by the scale length to get the fret-to-fret distance, or as an actual distance for a scale length of one.) The first-fret silent length, 1−1/r, is exactly t(0,1). Onward to other combinations of frets.
I've been using r for short as the twelfth root of two, but now it will help to write it out as 21/12. What's more, I was getting tired of writing 1/r so I'll just build that in and talk instead of the twelfth root of one half, ½1/12. Now the first-fret sounding part, scale length factored out, is just ½1/12, and the first-fret silent part is 1−½1/12. It's now easy to give the sounding length and silent length for any fret f:
Sounding length: ½f/12 Silent length: 1−½f/12
There are at least three ways to think of the fret-to-fret distance t(f1,f2):
f1 sounding length minus f2 sounding length: ½f1/12 − ½f2/12 f2 silent length minus f1 silent length: (1 − ½f2/12) − (1 − ½f1/12) f2−f1 silent length of f1 sounding length: ½f1/12(1−½(f2−f1)/12)
The last two both simplify to the first one, and all that's needed to adjust for any other number of frets per octave is to change the 12s.